John Schulman & Thinking Machines: LoRA utan ånger LoRA ersätter varje viktmatris W från den ursprungliga modellen med en modifierad version W'=W+γBAW'=W+γBA, där B och A är matriser som tillsammans har betydligt färre parametrar än W. LoRA fungerar på samma sätt som fullständig finjustering när: 1. LoRA tillämpas på alla lager i nätverket, särskilt MLP/MoE-lagren som innehåller de flesta parametrarna. 2. LoRA är inte kapacitetsbegränsat, d.v.s. antalet träningsbara parametrar överstiger mängden information som ska läras in, vilket kan uppskattas i termer av datauppsättningens storlek. Konsekvenser: Stora (t.ex. biljoner parametrar) basmodeller kan anpassas till en bråkdel av kostnaden för att träna en ny modell.

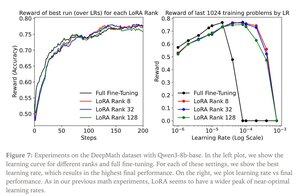
Inlägg från Thinking Machines: Gemini om beräkningskraven för LoRA på en gränsmodell - fortfarande formidabel, men antalet parametrar som används är mindre än 1 % av den totala modellstorleken (förträning).